BDS Software
Javascript Integer Operations
Floating-Point numbers are great. JavaScript loves them. In fact, Javascript loves them so much, that it doesn't really use any other kind of number at all.
W3 Schools (numbers) says:
JavaScript Numbers are Always 64-bit Floating Point:
Unlike many other programming languages, JavaScript does not define different types of numbers, like integers, short, long, floating-point etc.
JavaScript numbers are always stored as double precision floating point numbers, following the international IEEE 754 standard.
This format stores numbers in 64 bits, where the number (the fraction) is stored in bits 0 to 51, the exponent in bits 52 to 62, and the sign in bit 63.
But, sometimes you really want an integer. For example, if you're trying to simulate the inner-workings of some microprocessor, integers and integer operations are essentially indispensable. Many microprocessors use integers exclusively, and you just can't model them properly without using integers.
Now, Javascript does provide for some integer-type operations.
For example: i = 123; j = 456; k = i + j; --> k = 579.
And printing k will indeed report that it equals 579 = 0x243 (hexadecimal) = 10 0100 0011 binary.
But it is not stored as 10 0100 0011.
It's actually stored as 0100 0100 0001 0000 1100 0000 0000 0000 = 0x4410C000 (hex).
This is the IEEE 754 double precision floating-point representation of decimal integer 579.
cf. H. Schmidt's IEEE-754 Floating Point Converter.
Furthermore, n = Math.trunc(123.456); --> n = 123 -and- n = Math.round(123.456); also --> n = 123.
So...
We can just use Math.trunc or Math.round and we'll have all the integers we want. Right?
Well...
Not quite.
-----
Suppose we'd like a really large (i.e. 64-bit) integer; say something like:
6,913,015,601,128,030,207 = 0x 5FEF F70F FFF8 3FFF (hex)
= 0101 1111 1110 1111 1111 0111 0000 1111 1111 1111 1111 1000 0011 1111 1111 1111 (binary).
Try it yourself. Put the decimal number (without the commas, i.e. 6913015601128030207) into the textbox and then click the "ENTER" button to the right of the textbox:
Results:
-----
The problem here is that there is a loss of accuracy: you cannot accurately represent a 64-bit integer in the 64-bit IEEE 754 double precision floating-point format.
MDN Web Docs says that:
The maximum safe integer in JavaScript = 253 - 1, and
The minimum safe integer in JavaScript = -(253 - 1)
so that the maximum safe size of an integer in the 64-bit IEEE 754 format is 53 binary digits, not 64.
And, this also indicates a further deficiency. Try entering the even larger 64-bit hexadecimal integer 0xFFEFF70FFFF83FFF in the textbox above.
The correct (decimal) numerical equivalent would be -4513426513051649.
Yes, that's right! The proper result is negative.
Bit 63 is the sign bit and, when set, that bit indicates that the number is negative.
cf. https://en.wikipedia.org/wiki/Two%27s_complement.
-----
Even if we could cram a 64-bit integer into the IEEE 754 double precision format, we'd still face a couple of difficulties.
Try it yourself. Put 207915002490825 in the first textbox. Then put 172657863369673 in the second textbox. Then click the "AND" button.1. If we want to add two 64-bit numbers, we have to be able to tell when there has been a carry out of the 64th bit (bit 63 in the usual 0-63 bit numbering scheme). We can't do that if we have only 64 bits to work with. We'd need a 65th bit to hold that carry. For example, if we were limited to two decimal digits and tried to add 95+33=128, we couldn't do it because 128 won't fit into two decimal digits.
2. If we want to perform logic operations, such as bitwise AND, OR, XOR, NOT, or SHIFT, we're further limited because Javascript won't do that in 64 bits; it won't even do it in 53 bits - it's limited to 32 bits for such operations.
W3 Schools (bitwise) says:
JavaScript Uses 32 bits Bitwise Operands:
JavaScript stores numbers as 64 bits floating point numbers, but all bitwise operations are performed on 32 bits binary numbers.
Before a bitwise operation is performed, JavaScript converts numbers to 32 bits signed integers.
After the bitwise operation is performed, the result is converted back to 64 bits JavaScript numbers.
Results:
-----
The two numbers in the textboxes are each 48-bit numbers. But, the result is a 32-bit number. The upper 16 bits have been lost in the conversions.
Now, put 4225626057 in the first textbox, and 247407563 in the second textbox, and click the "AND" button. Note that you get the same result with these two 32-bit numbers that you did with the two 48-bit numbers earlier.
The "OR" and "XOR" buttons are provided to allow you to do some experimenting on your own.
Input can be decimal, hexadecimal (0x prefix, e.g. 0x2F3B87AA), or binary (0b prefix, e.g. 0b1101111101011101).
-----
The conclusion to be drawn from all of this is that, if we want to work with 64-bit integers in Javascript, we're going to have to limit our direct operations to 32-bit integers, and then form 64-bit integers out of two 32-bit integers via multiple precision arithmetic, i.e. with a 32-bit high-bits part and a 32-bit low-bits part. (cf. e.g. Warren; and/or cf. Neapolitan and Naimipour; and/or also TAMU).
For example:
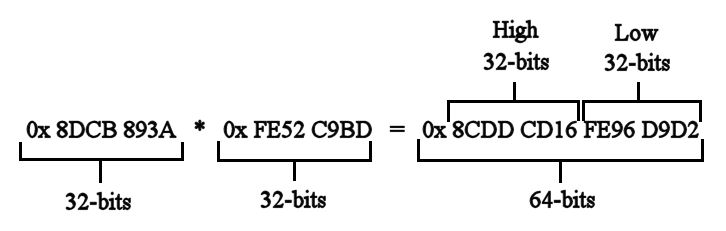
Since all numbers in Javascript are stored as 64-bit floating-point, this means we will have to literally waste 32 bits of every number we use. But, that's just the price we have to pay if we want to work with integers in Javascript.
(That can and will get even worse: to model a byte addressable microprocessor, we'll generally be wasting 56 bits of every 64-bit number).
Hopefully, we'll delve more deeply into multiple precision integer operations as we experiment with and develop a simulation of a MC6809 processor.
----------
But, for now, to see more details on how this all works, just right-click this page and then click on "View Page Source" (in FireFox - other browsers vary slightly but are generally similar).
M.D.J. 2018/12/13
----------References:
MDN Web Docs. https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Number.
Neapolitan, Richard and Naimipour, Kumarss (1998). Foundations of Algorithms Using C++ Pseudocode. Boston: Jones and Bartlett. pp. 71-78.
Schmidt, H., IEEE-754 Floating Point Converter https://www.h-schmidt.net/FloatConverter/IEEE754.html.
TAMU (Texas A&M University). Analysis of Algorithms, Lecture 20: Large Integer Arithmetic. http://faculty.cse.tamu.edu/djimenez/ut/utsa/cs3343/lecture20.html.
W3 Schools (bitwise). https://www.w3schools.com/js/js_bitwise.asp.
W3 Schools (numbers). https://www.w3schools.com/js/js_numbers.asp.
Warren, Henry S. Jr. (2003). Hacker's Delight. Boston: Addison-Wesley. pp. 34-37, 129-133, 140-145.