BDS Software

Spherical Maps

Maps for board wargames (including computerized equivalents of board wargames) are usually flat surfaces. But, the Earth is not flat. The Earth is round.

Currently, the Geographical Informations Systems (GIS) community refers to the shape of the Earth as a geoid. In the past, before GIS, it was called an oblate spheroid.

Game maps often cover only a small portion of the Earth's surface, and so a flat map is considered to be a workable approximation. And, so it should be: We have to use models and abstractions of reality in our game designs. Otherwise, our gameplay will become mired in a plethora of inconsequential details, and won't be fun anymore."

But, as the distances covered by the game map approach the size of the entire Earth, such models and abstractions begin to break down. (Yes, I know! But we wouldn't be game designers if we didn't occasionally entertain grandiose ideas, now would we?)

Or, think about this: Suppose you are the Commanding General of an Infantry Division on station at Kindo in the Democratic Republic of Congo. You are ordered to move 60 miles due East. You have just covered about 1.0 degree (out of 360.0) of the circumferance of the Earth at very near the Equator.

But now suppose you make a rude remark to the President of the United States, and suddenly find yourself transferred to Thule Airbase in northern Greenland. You're again ordered to move 60 miles due East. You have just covered about 4.3 degrees (out of 360.0) of the ~76.5 degree North Latitude circle around the Earth.

And now suppose you're stationed even further North at 89.5 degrees North Latitude. You get a another order to move 60 miles due East. You have just covered about 114.6 degrees out of 360.0 (almost a third of the way around the World at that Latitude) and you have drowned in the Artic Ocean just north of the Kana Sea in central Russia.

Or, equally fascinating, suppose you're an Airforce Colonel based in New York and you're ordered to fly your Wing to Madrid, Spain. On a plain flat map, it would appear that a direct flight due East all the way would be the shortest route. But, in actuality, the Great Circle Route is the shortest course between the two points on the surface of the Earth.

-----

Let's consider a couple of maps of the World. First, the common Mercator Projection which (at least when I was young [Yes, I know: pre-pleistocene]) was on the wall of every school room:

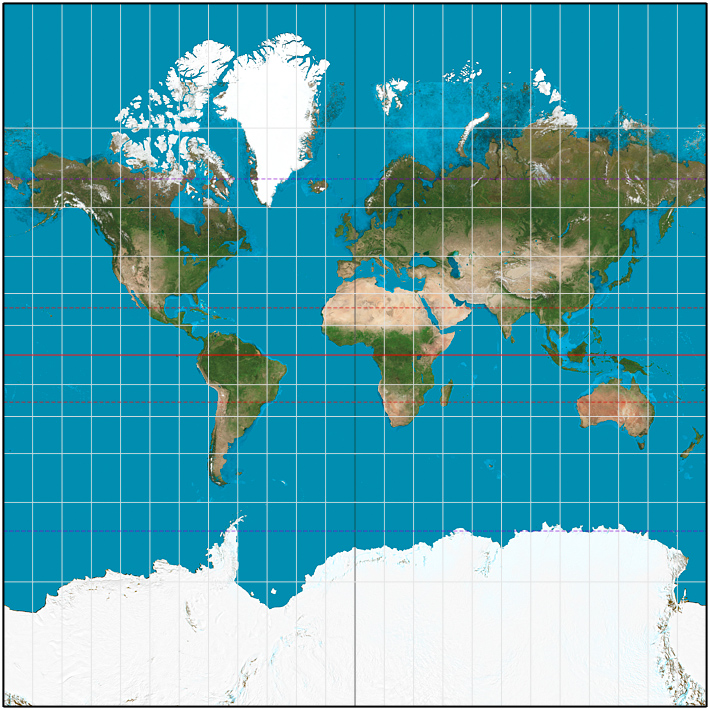
Mercator projection between 85°3'4"S and 85°3'4"N.
(Wikimedia Commons - Mercator)

Note how the white 15-degree lines, which produce squares near the Equator, produce greatly elongated rectangles as we near the poles. In fact, these rectangles become infinitely high at the poles - which is why the Mercator Projection shown here doesn't extend all the way to 90°N or 90°S.

The Mercator projection is a cylindrical map projection presented by the Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as straight segments that conserve the angles with the meridians. Although the linear scale is equal in all directions around any point, thus preserving the angles and the shapes of small objects (which makes the projection conformal), the Mercator projection distorts the size of objects as the latitude increases from the Equator to the poles, where the scale becomes infinite. So, for example, landmasses such as Greenland and Antarctica appear much larger than they actually are relative to land masses near the equator, such as Central Africa. (Wikipedia - Mercator).

Thus, I concluded that a Mercator Projection would not be useful for my game design purposes, because it could never actually encompass the entire Earth.

Now, let's look instead at the Plate Carrée Projection which is used in a lot of modern GIS work:

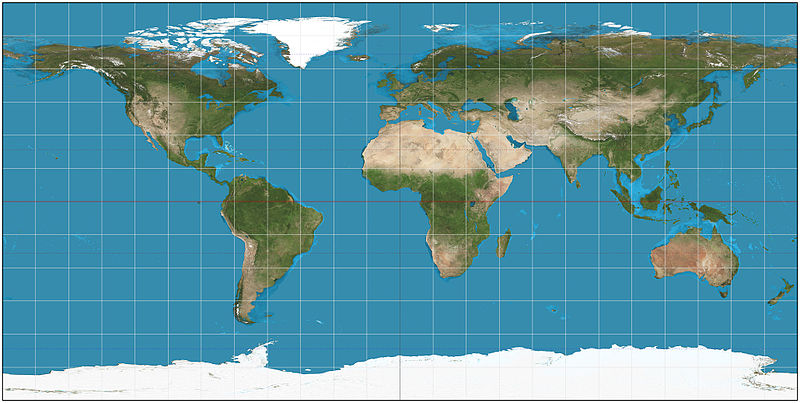
The world on plate carrée projection.
(Wikimedia Commons - Equirectangular)

Note how the white 15-degree lines produce uniform squares all across and up and down the entire map. That's what "Equirectangular" essentially means. And, note how the map extends all the way to 90°N and 90°S.

The equirectangular projection (also called the equidistant cylindrical projection, geographic projection, or la carte parallélogrammatique projection, and which includes the special case of the plate carrée projection or geographic projection) is a simple map projection attributed to Marinus of Tyre, who Ptolemy claims invented the projection about AD 100. The projection maps meridians to vertical straight lines of constant spacing (for meridional intervals of constant spacing), and circles of latitude to horizontal straight lines of constant spacing (for constant intervals of parallels). The projection is neither equal area nor conformal. Because of the distortions introduced by this projection, it has little use in navigation or cadastral mapping and finds its main use in thematic mapping. In particular, the plate carrée has become a standard for global raster datasets, such as Celestia and NASA World Wind, because of the particularly simple relationship between the position of an image pixel on the map and its corresponding geographic location on Earth. (Wikipedia - Equirectangular).

The uniform squares of the Plate Carrée Projection can, of course, be subdivided into smaller uniform squares which, in turn, can be further subdivided into even smaller uniform squares, thus producing a Squares Scenario computerized game board representing the entire World.

Every map shows distortions. After all, we're trying to display a round ball on a flat sheet. But the distortions of the Plate Carrée Projection produce a playable map that I feel I can make good use of.

And, what appears distorted to the human player, doesn't have to appear distorted to the computer. And, vice-versa: what appears to the human player to be uniform squares, doesn't have to appear as such to the computer. In fact, I propose to make the squares look like non-uniform trapezoids to the computer; trapezoids which will degenerate into triangles at the poles.

-----

Now, while the computer is quite capable of handling geoids and oblate speroids, the actual shape of the Earth (and of other planets as well) does not appreciably vary from that of a perfect sphere. Therefore, in the interests of simplifying gameplay, I have chosen to model planets as perfect spheres.

So, assuming the Earth to be a perfect sphere, when it is mapped to a Plate Carrée Projection (Equirectangular), the represented East-West x-distances along the parallels (i.e. circles of latitude) will be a function of the latitude, i.e.

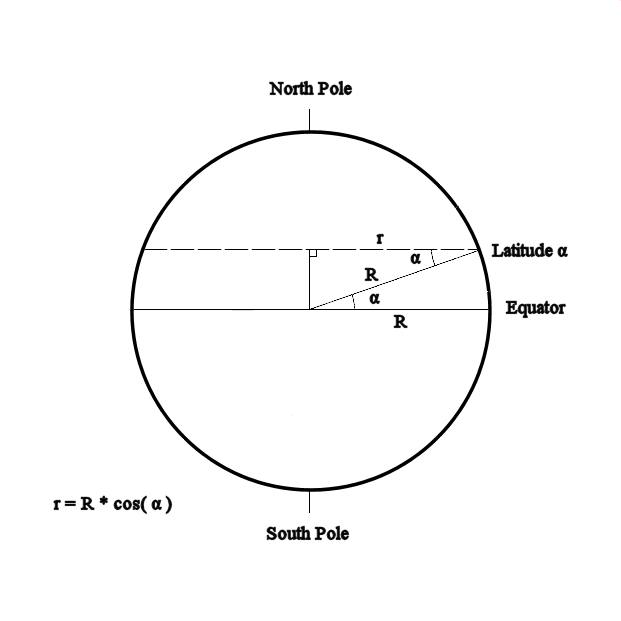
Earth - Side View.

The radius at the Equator will be one Earth radius, and the radii at the poles will be zero. The radius at any given latitude will be
r = R * cos ( α ) where α is the latitude angle.

The Earth is nominally of Circumferance = 24,902 miles. One mile = 5,280 feet. One nautical mile = 2,000 yards = 6,000 feet. Thus 24,902 miles * (5,280 feet/6,000 feet) = 21,914 nautical miles. And, at 360° per circle, each degree would =~ 60.87 nautical miles.

So, let us model the Earth at the round number of 60 nautical miles per degree. This would imply that each (circular) minute will equal 1 nautical mile, each (circular) second will equal 100 feet, and the model's circumferance at the Equator will be 21,600 nautical miles.

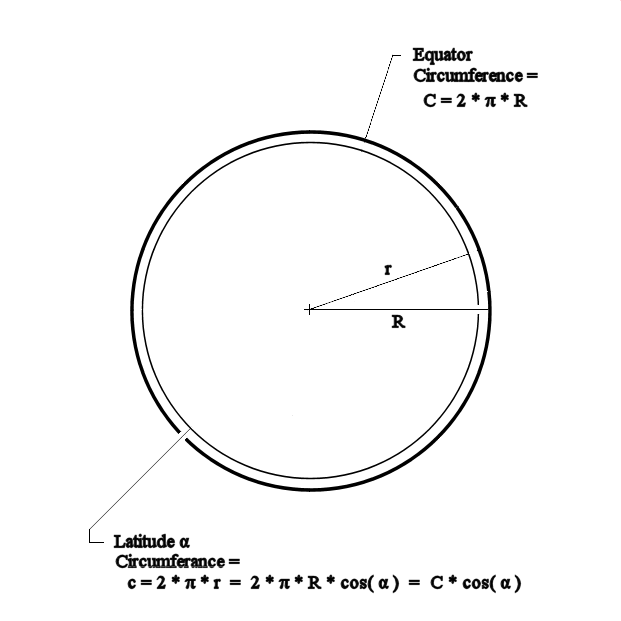
Earth - Top View.

This will allow us to model almost any portion of the Earth's surface in squares with dimensions in round numbers.

Suppose we want to model the entire Earth for a Grand Startegic conflict situation, perhaps in some ways analogous to the game of Risk. And, suppose we want our map squares to represent 15°. Each square's sides will then represent a length of 15 * 60 = 900 nautical miles, and our 180° x 360° world map will encompass 12 * 24 = 288 squares.

Eventually, we're going to need a significantly large database to organize the information included on the spherical map. But, for now, let's just consider what we need for a plain spherical map with no details. We need to identify each square, we need to identify each square's eight neighbors, we need to identify the distance from the center of the square to the centers of each of its eight neighbors, and we need to identify the facing that a unit in the square will have after moving to each of the square's eight neighbors.

I propose to use 4-byte integers for everything in this database. We could use 4-byte floats for distances (we don't need the precision of 8-byte doubles), but integers are better for comparisons. For example, suppose we calculate float A = 0.0000001 and then use the pseudo-statement "if A == 0 then do something". Technically, A is not equal to zero, but it might as well be for our purposes.

I thus propose to express distances as integers, in feet. For example, suppose we calculate the distance between two squares as 23.247653 nautical miles. 23.247653 * 6,000 = 140,925.918 feet. This would be stored in the database as 140,926 feet. The loss of precision in this conversion is negligible.

Using 4-byte integers for everything, we can generally specify each square's data as follows:

Field	Bytes
Auto-Increment Primary-Key	4
Square's x-coordinate	4
Square's y-coordinate	4
Neighbors' x-coordinates	32
Neighbors' y-coordinates	32
Neighbors' distances	32
Neighbors' facings	32
	----
Total bytes per square	140

288 squares * 140 bytes per square = 40,320 bytes total.

Suppose, instead, that we want the squares to be one degree on a side [60 nautical miles]. Then, the map will be 180 x 360 = 64,800 squares ==> 9,072,000 bytes =~ 8.65 megabytes.

If we want squares with one (circular) minute on a side [1 nautical mile = 6,000 feet], we'll have 10,800 x 21,600 = 233,280,000 squares ==> 32,659,200,000 bytes =~ 30.42 gigabytes.

And, if you're hoping for squares that are one (circular) second [100 feet] on a side, you'd better have one honking big and fast computer, because that'll require 648,000 x 1,296,000 = 839,808,000,000 squares ==> 117,573,120,000,000 bytes =~ 106.93 TERAbytes!

However, I suspect that if we want small squares, we're probably NOT going to be trying to model the entire Earth at once.

So, for now, let's stick with the more practical "one degree on a side" map requiring 8.65 megabytes.

But we might now ask a question: While terrain features, etc. will not be uniformly distributed over our squares, and thus should indeed be stored in a database; the directed distances between plain squares are quite uniform -- would it be faster to access these values from a database, or to calculate them in code? We'll explore this question on this site's Database vs. Code page.

                                                                                                                                                                M.D.J. 2018/05/24

----------

References:

Wikipedia - Mercator. https://en.wikipedia.org/wiki/Mercator_projection.

Wikipedia - Equirectangular. https://en.wikipedia.org/wiki/Equirectangular_projection.

Wikimedia Commons - Mercator. https://commons.wikimedia.org/wiki/File:Mercator_projection_Square_lo-res.JPG.

Wikimedia Commons - Equirectangular. https://commons.wikimedia.org/wiki/File:Equirectangular_projection_SW.jpg.